Piecewise-linear tracing utility for implicitly defined curves

Example: Fixpoints

Let \( g: \mathbb{R}^n \rightarrow \mathbb{R}^n, g_k(x) = \exp\Big( \cos\Big( k \cdot \sum\limits_{i=1}^n x_i \Big)\Big) \) for \(k = 1,\ldots,n\)

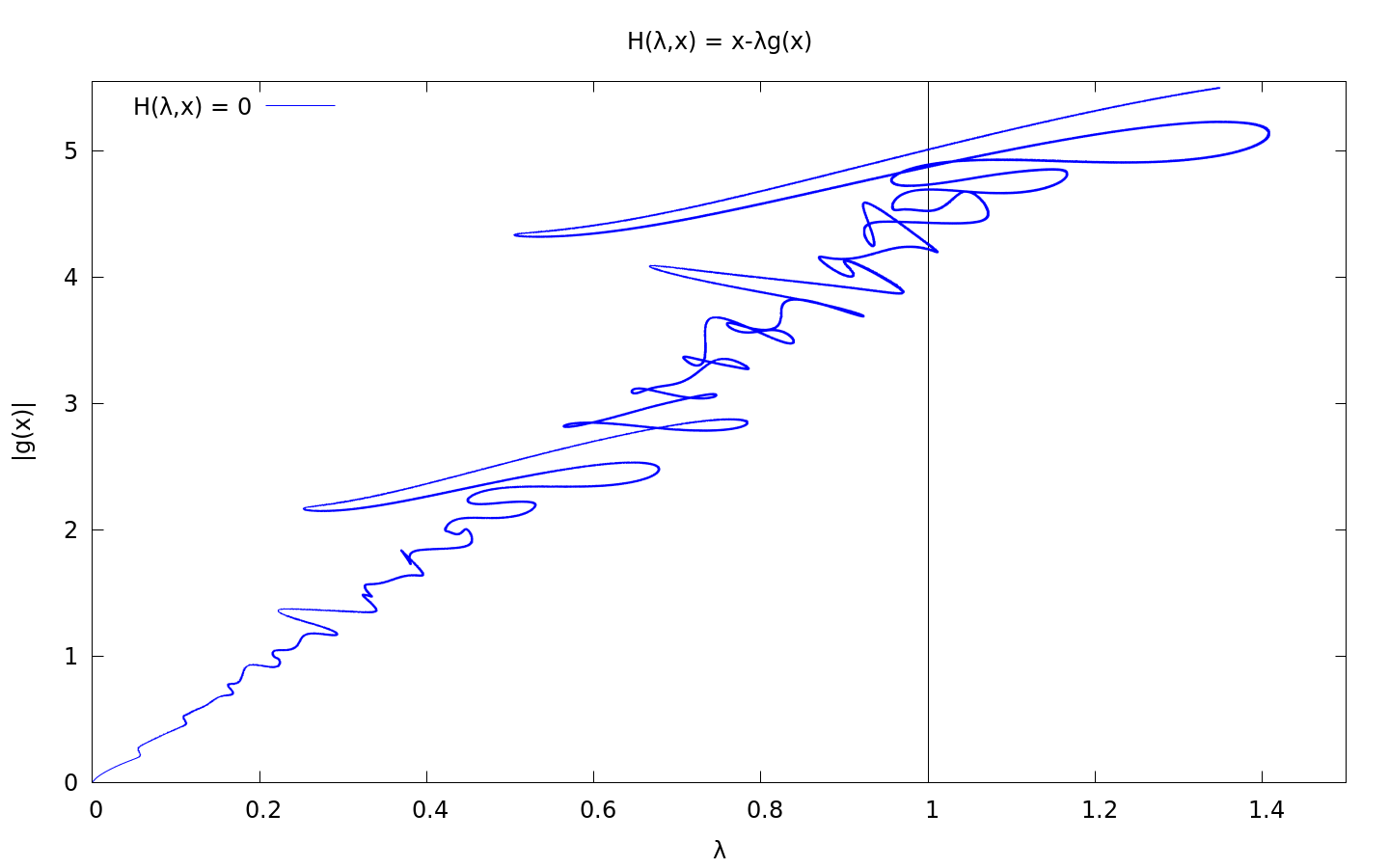
Considering the homotopy

$$H:[0,1] \times \mathbb{R}^n \rightarrow \mathbb{R}^n, (\lambda,x) \mapsto x - \lambda g(x)$$

it is obvious, that \(H(0,x) = x\) and \(H(1,x) = 0 \Leftrightarrow x = g(x)\) One approach to find fixpoints of \(g\) is therefore to follow \(H^{-1}(0)\) starting at \(x=0\) until \(\lambda = 1\) holds. traceu provides piecewise linear approximations of such curves with upper bounds for the error enabling further (e.g. newton-type) methods to be successfully applied on the results. The picture above depicts a trace of \(H^{-1}(0)\) for \(n=10\).

About the Project

• Still beta, development is quite stale.
• Written in C.
• Quite unrestrictive regarding input requirements (e.g. no derivability needed).

Todo

• Multithreading.
• An input parser to get rid of recompiling for every problem.
• A GUI would be nice, something written in ncurses would do perfectly fine.